A. Glazman, "Discrete Probability in models of Mathematical Physics"
A.A. colours each face of the hexagonal lattice in yellow or blue independently: in yellow with probability p; in blue with probability 1-p.
V.V.: Will there be an infinite connected component of yellow faces?
A.A.: Depends on p: there is almost surely a unique infinite component when p > 1/2 and there is no infinite component otherwise. The model is called Bernoulli percolation.
V.V.: How do interfaces between yellow and blue components look like at p = 1/2?
A.A.: Like a random fractal SLE6! We will prove this seminal theorem of Smirnov.
V.V.: What if the colours of faces are not independent?
A.A.: Then you can get the Ising model for ferromagnetism: define the distribution to be proportional to e^(−1/T) to the number of pairs of adjacent faces of different colour.
V.V.: Hm... only neighbours interact? Won’t we get percolation on far away faces?
A.A.: Only for large T! The transition occurs at Curie temperature Tc: when T < Tc, one of the colours dominates. Convergence to SLE6 when T > Tc is a big conjecture.
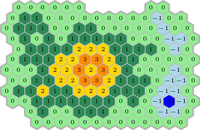
V.V.: What if we put integer numbers instead of colours?
A.A.: View numbers as heights and get a random surface! We will discuss the uniform distribution on Lipschitz functions: they differ by 0, 1, or −1 at adjacent faces. They are conjectured to converge to the Gaussian Free Field.
Background. Though these models have simple definitions, they allow to construct deep mathematical theories. The growing interest to lattice models is confirmed with Fields Medals to Werner (2006) and Smirnov (2010). Also, Berezinskii–Kosterlitz–Thouless phase transition in the XY model was awarded Nobel Prize in Physics in 2016.
Open problems. There are a lot of new questions of various difficulty — some could become a subject for a Bachelor/Master/PhD thesis.
Prerequisites. Introduction to Probability Theory. No previous knowledge of Physics/Mathematical Physics is assumed.

